The Mysterious Case of the Cases (2.3)
Who would have imagined I would get to the third post in this series?? I put a trip to an all-you-can eat pizza place as a bet with myself that I would drop out by the second post. Guess I'll have to pay...
In any case, here's the third problem in Terry Tao's book:
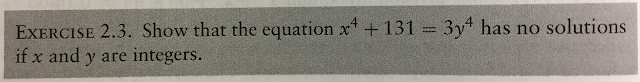 |
| Sorry, no hint this time! |
In following with the number theory problems, we encounter a fairly standard-looking Diophatine equation. Instead of finding the solutions though, the goal is to show there are no solutions.
A quick look at Wolfram told me $131$ is a prime number (and that it divides $53^5-1$). The former could be important since, as Terry himself describes, factorizing is one of the main strategies when facing equations on the integers. For example, we can rewrite the equation as:
\[ \begin{equation} \label{(1)} 3y^4-x^4 = 131 \end{equation} \]
Then, if we could factorize the LHS into some $A \cdot B$:
Then, if we could factorize the LHS into some $A \cdot B$:
$A \cdot B = 131$
Since $131$ is prime, the only possible values for the factors would be the $(A,B)$-pairs:
The problem then becomes showing that there are no integer solutions for $A$ and $B$; the advantage being we have two equations of two unknowns with smaller degrees to work with.
$(-131,-1)$, $(-1,-131)$, $(1,131)$, and $(131,1)$.
The problem then becomes showing that there are no integer solutions for $A$ and $B$; the advantage being we have two equations of two unknowns with smaller degrees to work with.
The issue is that the LHS can't be factorized (that $3$ gets on the way of anything nice), so I quickly abandoned the factorization route.
--------------------------------------------
As we saw in the last problem, another good strategy is to use mods to find cases the variables must (or in this case can't) verify. Mods and powers mix pretty well after all!
It doesn't take long to see that the most obvious ones to try, like $131$ or $3$, don't give much though. Take $3$ as an example of what happens. Writing $\eqref{(1)}$ in (mod $3$):
It doesn't take long to see that the most obvious ones to try, like $131$ or $3$, don't give much though. Take $3$ as an example of what happens. Writing $\eqref{(1)}$ in (mod $3$):
$-x^4 \equiv 2 \ [3]$
$x^4 \equiv 1 [3]$
So now we know that $x^4$ must have a residue of $1$ when divided by $3$. In (mod $3$) there are only three cases to check for $x$ itself:
- $x \equiv 0 \ [3] \ \implies \ x^4 \equiv 0 \ [3]$
- $x \equiv 1 \ [3] \ \implies \ x^4 \equiv 1 \ [3]$
- $x \equiv 2 \ [3] \ \implies \ x^4 \equiv 1 \ [3]$
This means $x$ can't be a multiple of $3$, which we already knew since otherwise $3$ would be a factor of $131$...
At this point, the $4$ in the exponents gave me a hunch that (mod $5$) would be a good candidate to try because of Fermat's little theorem; it indeed ends up working (the end is left as an exercise for the reader). However, unless you studied some number theory, you won't know about it.
Even without this knowledge, we could still have kept trying other mods; $5$ is small enough that it wouldn't take long to bump into it if you just keep experimenting. This is not necessarily a wild guess though: $5$ is a reasonable mod to look at since it is a small prime and $131 \equiv 1 [5]$, which is a rather nice number to work with.
That being said, I wanted to find a second way that didn't depend on finding the right mod, but still used a cases strategy.
With that in mind, what other type of cases could we look at? Since we're looking at fourth powers, it makes sense to see if there's anything particular about them; for example their endings. The last digit of any power only depends on the last digit of the original number, so there are only 10 cases for last digits:
At this point, the $4$ in the exponents gave me a hunch that (mod $5$) would be a good candidate to try because of Fermat's little theorem; it indeed ends up working (the end is left as an exercise for the reader). However, unless you studied some number theory, you won't know about it.
Even without this knowledge, we could still have kept trying other mods; $5$ is small enough that it wouldn't take long to bump into it if you just keep experimenting. This is not necessarily a wild guess though: $5$ is a reasonable mod to look at since it is a small prime and $131 \equiv 1 [5]$, which is a rather nice number to work with.
--------------------------------------------
That being said, I wanted to find a second way that didn't depend on finding the right mod, but still used a cases strategy.
With that in mind, what other type of cases could we look at? Since we're looking at fourth powers, it makes sense to see if there's anything particular about them; for example their endings. The last digit of any power only depends on the last digit of the original number, so there are only 10 cases for last digits:
$z$ $z^4$ $3z^4$
$0$ $0$ $0$
$1$ $1$ $3$
$2$ $6$ $8$
$3$ $1$ $3$
$4$ $6$ $8$
$5$ $5$ $5$
$6$ $6$ $8$
$7$ $1$ $3$
$8$ $6$ $8$
$9$ $1$ $3$
Looking at this, is there any way for $3y^4 -x^4$ to have the last "$1$" of $131$ as a last digit?
The only way for that to be possible is if the $0, 3, 5, 8$ in the third column can give a $1$ after being subtracted by a digit of the second column.
However, the last digit values that substracted from the third column give $1$ are $9, 2, 4, 7$ respectively; numbers that are missing from the second column!
In other words, $3y^4 -x^4$ can never have a $1$ as a last digit, which implies that there are no integers that could verify $3y^4-x^4 = 131$ $\square$
Two different solutions for the problem, not too bad!
You may be thinking it's ironic that a post about solutions leaves one of them unfinished. It is, but knowing which mod to use and an example of how it could be applied is already more than 85% of the work at this point. The main difficulty here would be to pick the correct mod to use, but as mentioned above, there would be good reasons to try that one. Once again we bare witness to the power of modular arithmetic; I really think it could use a much bigger role in secondary education.
As for the second solution, putting aside the fact that I wanted the post to be a bit longer than if I had just showed the solution using mods, I felt it could be useful to show other things we can look at while solving these number theory problems.
As a matter of fact, these two ways are not really that different. Looking at the $z^4$ column, we can see why (mod $5$) would be nice to explore: those numbers are either $0$ or $1$ (mod $5$). Both methods actually boil down to the same!
One last cool thing. Both solutions, exactly as they are written, can actually prove something much stronger:
If that had been the problem, I wonder if it would have gone that smoothly? With that last question in the air, see you next time!
Looking at this, is there any way for $3y^4 -x^4$ to have the last "$1$" of $131$ as a last digit?
The only way for that to be possible is if the $0, 3, 5, 8$ in the third column can give a $1$ after being subtracted by a digit of the second column.
However, the last digit values that substracted from the third column give $1$ are $9, 2, 4, 7$ respectively; numbers that are missing from the second column!
In other words, $3y^4 -x^4$ can never have a $1$ as a last digit, which implies that there are no integers that could verify $3y^4-x^4 = 131$ $\square$
Two different solutions for the problem, not too bad!
 |
| It is indeed true there were no exotic cases this time but still... |
You may be thinking it's ironic that a post about solutions leaves one of them unfinished. It is, but knowing which mod to use and an example of how it could be applied is already more than 85% of the work at this point. The main difficulty here would be to pick the correct mod to use, but as mentioned above, there would be good reasons to try that one. Once again we bare witness to the power of modular arithmetic; I really think it could use a much bigger role in secondary education.
As for the second solution, putting aside the fact that I wanted the post to be a bit longer than if I had just showed the solution using mods, I felt it could be useful to show other things we can look at while solving these number theory problems.
As a matter of fact, these two ways are not really that different. Looking at the $z^4$ column, we can see why (mod $5$) would be nice to explore: those numbers are either $0$ or $1$ (mod $5$). Both methods actually boil down to the same!
One last cool thing. Both solutions, exactly as they are written, can actually prove something much stronger:
The equation $x^4 + 10k+1 = 3y^4$ has no solutions
for $x, y \in \mathbb{Z}$ and $k \in \mathbb{N}$.
If that had been the problem, I wonder if it would have gone that smoothly? With that last question in the air, see you next time!


Comments
Post a Comment